|
π, FE EN EL CAOS (1998) (Pi: Faith in Chaos) Ficha técnica Duración: 1:20:21 Director: Darren Aronofsky Reparto: Sean Gullette, Mark Margolis, Ben Shenkman, Pamela Hart, Stephen Pearlman Música: Clint Mansell (basada en Rap y hip hop) Guión: Darren Aronofsky, Sean Gullette Producción: Eric Watson Fotografía: Matthew Libatique (B/N, grano) Nacionalidad: Estados Unidos
|
|
|
|
Trata sobre las relaciones de un matemático "prodigioso", con fuertes migrañas, encerrado en sí mismo, desequilibrado con el medio que le rodea y su progresiva e irremediable obsesión con la teoría de los números... |
|
Sinopsis (Advertencia: Esta sección contiene detalles de la trama y el argumento)
|
Max es un matemático obsesionado por encontrar el código numérico que rige el aparente caos del mercado bursátil. Pero primero ha de encontrar el valor del número pi. Afectado periódicamente por unas brutales jaquecas, mientras investiga se cruzan en su camino una agresiva firma de Wall Street y una secta judía interesada en descifrar los secretos de los textos sagrados. Ambos se interesan por Max pues creen firmemente que sus investigaciones son de gran valía para sus propios intereses.
Objetivos didácticos generales: - Apreciar las matemáticas como algo que puede integrarse con normalidad en la cotidianidad de las personas (cine). - Analizar la diferente galería de arquetipos matemáticos que aparecen: (el matemático veterano; matemático obsesivo; el hábil calculista) - Valorar la importancia de trabajar en equipo con actitud de cooperación, tolerancia y solidaridad. - Utilizar los distintos medios tecnológicos, calculadora y ordenador, para realizar cálculos y buscar información de diferentes tipos. En esta película iremos intercalando escenas de contenido matemático con la sinopsis:
Los títulos de crédito ya por si solos son matemáticas en estado puro.
Ø Define que es un número racional y un número irracional. Escribe dos ejemplos de cada uno de ellos. Ø ¿Cómo se llama el conjunto numérico que contiene a los números racionales e irracionales? Ø Piensa un número que no sea racional ni irracional. Ø En la secuencia que acabas de ver, van apareciendo todos los decimales del número pi. Escribe los 10 primeros decimales. ¿Podrías alguna vez escribir los dos últimos? ¿Por qué? Ø Detenemos la imagen cuando aparezca la banda de Mobius y la explicamos para que la entiendan, sin entrar en demasiadas explicaciones matemáticas. Les enseñamos la obra de Escher (Competencia cultural y artística) y les enseñamos a construir con una tira de papel una banda. ¿Qué relación crees que tienen la banda de Moebius y el número pi? (Competencia aprender a aprender)
"Las nueve y media, apunte personal, cuando era pequeño mi madre siempre me decía que no mirase nunca al sol, pero a los seis años, lo hice. Los médicos no sabían si quedaría ciego. Estaba aterrorizado. Solo en la oscuridad...
- Max, Max, ¿quieres hacerlo? -dice la niña- ¿Cuánto da 322 por 491? - 158102 - responde de inmediato. - ¡Bieeeen! -comprobándolo con la calculadora.
- ¿Y cuánto da 73 entre 22?? - 3,3181818... - va diciendo indefinidamente mientras se aleja. Ø Comprueba con la calculadora que son correctas las dos operaciones que propone la niña a Max. Ø En el caso del primer resultado: 158102 ¿qué tipo de número es? ¿a qué conjuntos numéricos pertenece este número? Calcula su correspondiente descomposición factorial. Ø En el caso del segundo resultado: 3,318181818… ¿qué tipo de número es? ¿a qué tipo de conjuntos numéricos pertenece este número? Exprésalo en forma de fracción. Realiza una aproximación a la unidad, décima, centésima y milésima.
" Las matemáticas son el lenguaje de la naturaleza". "Todo lo que nos rodea se puede representar y entender mediante números".
- Si se hace un gráfico con los números de un sistema se forman modelos. Estos modelos están por todas partes en la naturaleza... veremos emerger patrones. - ¿Y la bolsa? Una infinidad de números que representa la economía global. Millones de manos trabajando, millones de mentes. Una red inmensa llena de vida. Un organismo. Un organismo natural. La bolsa también forma un modelo.
Ø De las tres afirmaciones que hace Max cuando camina por la calle, explica las dos primeras poniendo ejemplos (competencia en conocimiento e interacción con el medio físico) Ø Busca en Internet lo que significa la palabra hipótesis, tesis, axioma, conjetura y teorema. Escribe el enunciado de un Teorema que conozcas y busca en internet alguna conjetura que todavía no se haya demostrado. (Competencia digital y tratamiento de la información). Ø ¿Cuál es la hipótesis que enuncia Max al final de la escena? Ø Después de la visualización de esta escena, describe en un mínimo de 10 líneas cómo crees que es la personalidad de Max. (Competencia Lingüística, autonomía e iniciativa personal)
Maximillian Cohen es un brillante Matemático, especialista en la rama computacional, paranoico e inseguro que sufre continuos dolores de cabeza -MIGRAÑAS- dicen los críticos que fruto de su vida encerrada y silenciosa. Como consecuencia de esto, de sus miedos y dudas existenciales, vive en un piso con seis cerraduras y un súper ordenador de cálculos. Además, no soporta el contacto humano salvo con un anciano profesor con el que juega al ajedrez chino.
Max pretende descubrir el modelo matemático de la bolsa a través de cálculos y programas propios que introduce en su ordenador Euclides. Ø ¿Qué relación une a Max y a su compañero de juego? (Competencia aprender a aprender) Ø Busca en Internet el nombre del juego que aparece en la escena y explícalo brevemente. (Competencia digital y tratamiento de la información) Ø Investiga en Internet quién era Ícaro y resume la información (Competencia digital y tratamiento de la información, competencia cultural y artística, competencia lingüística) Ø Explica por qué el antiguo profesor de Max le dice: “en la vida hay algo más que matemáticas” (competencia lingüística) Ø Cuando Max va en el metro, escribe dos fórmulas en un periódico. ¿De qué fórmulas se tratan?, ¿por qué crees que las dibuja? Representa ambas en tu cuaderno. Ø Busca en Internet por qué se representa al número pi con la letra griega p.(Competencia digital y tratamiento de la información)
Se aprecia la relación entre la Torah y los números.
El judío Rabbi Cohen presenta la teoría en hebreo trascrito en números en la cual el personaje Max Cohen relaciona esta última teoría con la secuencia de Fibonacci llegando en conclusión que todo esta basado en la ley del orden y el caos. Ø ¿Qué hace el judío cuando entra en la habitación dónde está Max y por qué crees que lo hace? (Competencia social y ciudadana) Ø Busca en Internet que es la Torah y haz un breve resumen. (Competencia digital y tratamiento de la información, competencia cultural y artística, competencia lingüística) Ø El judío le dice a Max que la Torá es un código enviado por Dios, ¿por qué crees que al número áureo también se le denomina la divina proporción? (Competencia aprender a aprender) Ø Escribe los quince primeros términos de la sucesión de Fibonacci, después realiza los cocientes entre los términos consecutivos y di a que número se aproximan estos cocientes. Ø Clasifica a que conjunto numérico pertenece el número áureo. Ø Busca en Internet por qué se representa al número áureo con la letra griega phi. (Competencia digital y tratamiento de la información) Ø Investiga en Internet la aparición de la sucesión de Fibonacci en la Naturaleza. (competencia en conocimiento e interacción con el medio físico)
La vida de Max se hace todavía más dura cuando descubre y relaciona el número que mueve la existencia de todo ser vivo: el número Pi. Tras hacer este descubrimiento comienza a ser perseguido por varios grupos que desean los servicios del matemático y la revelación de su secreto. Por una parte tenemos a una gran corporación de Wall Street que son los primeros en buscar a Max para encontrar un patrón que explique las variaciones de la Bolsa de Nueva York. Le ofrecen grandes sumas de dinero, pero él no lo quiere y le comienzan a perseguir. - No estoy interesado en su dinero. ¡Quiero entender nuestro mundo!
En una de estas persecuciones se encuentra con un grupo judío Hasidic, en un principio amables con el protagonista, incluso le llegan a redescubrir los secretos de las Matemáticas de la Torah. Pero al final también interesados en las fórmulas de la existencia y quieren el número de 216 dígitos, ya que creen que representa el verdadero nombre de Dios, que se perdió en la destrucción del segundo templo de Salomón.
- Si te empeñas en encontrar el 216, lo encontrarás por todas partes. Cuando tu mente se obsesiona con cualquier cosa desechas todo lo demás y sólo eres capaz de ver esa cosa. - Max, en el momento en que descartas el rigor científico, dejas de ser un matemático, y te conviertes en un numerólogo.
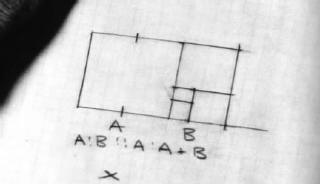
- i Las 4:42!. Más pruebas. ¿Recuerdas a Pitágoras? Matemático. Líder cultural de Atenas. Año 500 a.C. Su creencia: el universo se compone de números. Su contribución: la razón áurea, representada geométricamente por el rectángulo áureo. Existe una proporción visual en su forma y en sus dimensiones. Si se hace un cuadrado queda otro pequeño rectángulo áureo de las mismas proporciones. Se puede repetir el proceso con cuadrados cada vez menores hasta el infinito... 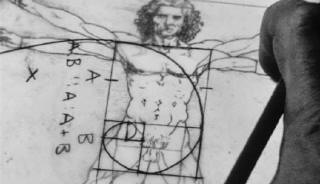-es interrumpido unos momentos por una llamada a la puerta de una hermosa chica, pero no abre- las 11:20, más pruebas, Leonardo Da Vinci, artista, inventor, escultor, naturalista, italiano, siglo XV, redescubrió el canon de la perfección con el rectángulo áureo, y lo plasmó en sus obras maestras. Si se traza una curva que une los rectángulos concéntricos se obtiene la mítica espiral áurea. Pitágoras adoraba esa forma. Está en toda la naturaleza: en las conchas, en los cuernos, en los remolinos, en los tornados, en las huellas dactilares, en el ADN... incluso en la Vía Láctea. Las 9 y media. Apunte personal: cuando era pequeño mi madre me decía que no mirara al sol. A los 6 años lo hice. Al principio el resplandor era intenso, pero eso ya lo sabía. Continué mirando sin parpadear... entonces el resplandor empezó a desaparecer, mis pupilas se contrajeron y lo vi todo con claridad... por un momento lo entendí.
Al final de la película, Max parece acertar el lugar que ocupa en el mundo, el grano de la película es más fino, la imagen más nítida. La niña parece heredar la obsesión de Max por los números y le pide volver a jugar con ellos. - ¿Cuánto da 255 por 183? -pregunta la niña con la calculadora en la mano -Yo ya lo sé. ¿Y tú, también lo sabes? - ¿Cuánto? - dice Max, moviendo negativamente la cabeza. - 46665. ¿Lo ves? ¿Y cuánto da 748 dividido por 238? ¡Yo lo sé! ¿Cuánto da? Este es un cociente matemáticamente interesante: si lo simplificamos da 22/7. Esta fracción se aproxima a p El 22 del 7 parece que es un día de fiesta en una cultura determinada. ¿Cuál? Más tarde, Max Cohen, consciente del perjuicio que le produce el estrés y las persecuciones decide simplificar su vida dejando a un lado su fórmula. El matemático llegó a tal punto donde su investigación y razonamiento no le reportaba ni felicidad ni paz, todo lo contrario, desequilibrio mental y paranoias. A veces hay que relajarse y no olvidarse nunca de la ciencia racional.
GAZAPOS - En la escena en la que aparecen las cifras decimales del número pi, las ocho primeras son correctas, pero a partir de la novena no lo son.
- En hebreo no existe el cero. - Cuando el amigo de Max comenta la densidad, dice que es el Peso/volumen. ¿Es cierto esto? - Los números bursátiles que aparecen sobre su ordenador se repiten cíclicamente. ¡Cuestión de presupuesto! Curiosidades El propio título de la película ya refleja de manera muy fiel qué es lo que nos vamos a encontrar en ella: Matemáticas y caos, mucho caos. Se trata de la ópera prima de Darren Aronofsy, considerado hoy en día como un director de culto de cine independiente estadounidense. Y todas las máximas del cine de este tipo se ven reflejadas a la perfección en el largometraje: nulo presupuesto (60000 $), cuatro decorados repetidos durante toda la película, actores que en muchos casos no son ni profesionales. La obra está íntegramente rodada en un blanco y negro muy sucio, contribuyendo a aumentar aún más esa sensación de producto “barato”, aunque el grano utilizado en el film realmente va en consonancia con el dolor que le producen las migrañas al protagonista. Gracias a un magistral trabajo de fotografía y a la bizarra banda sonora, el director consigue hacer que el desequilibrio mental del protagonista llegue a transmitirse al espectador de una forma total. Verdaderamente hay momentos de la película en los que sentiremos que nosotros mismos estamos locos. Los muchos minutos de voz en off con las reflexiones matemáticas, filosóficas y personales del antihéroe contribuyen en gran medida a esto. La paranoia y la realidad se mezclan indiscriminadamente a lo largo de la película, sin que ésta haga un especial esfuerzo por aclararnos en qué punto nos encontramos.
Muchas son las referencias subliminales al número pi:
Algunas menciones matemáticas explícitas o implícitas a lo largo del film: En la película, aparecen referencias al número áureo, a los números irracionales, a la secuencia de Fibonacci y a las vidas de Euclides, Pitágoras, Arquímedes de Siracusa y Leonardo da Vinci.
NOTA: Presiona (presionando previamente escape) aquí si quieres escuchar la música que suena son los primeros 1024 dígitos de Pi en hexadecimal, convertidos en notas musicales MIDI. Cada dígito se escucha como una nota distinta. Tiene una duración de 4 minutos y 16 segundos en total. Suena extrañamente bien para lo que cabría esperar de una secuencia bastante aleatoria como la que forman los dígitos de π. PREMIOS OBTENIDOS: 1998: Tercer puesto en el Fant-Asia Film Festival a la mejor película internacional. 1998: Premios Gotham al talento independiente, Palma Abierta a Darren Aronofsky. 1998: Premio a la dirección en el Festival de Cine de Sundance. 1998: Festival de Cine de Thessaloniki, Mención especial a Darren Aronofsky. 1999: Premio Chlotrudis de cine independiente a la mejor fotografía. 1999: Premio del Círculo de Críticos de Cine de Florida (FFCC) al descubrimiento del año: Darren Aronofsky. 1999: Premios Independent Spirit al mejor primer guión. 1999: Mención especial en la Semana Internacional de Cine Fantástico de Málaga por el guión.
http://www.neoteo.com/la-historia-de-pi.neo
ACTIVIDADES Taller - Laboratorio Nº 556<br />Proyecto : Reingeniería Pedagógica en la didáctica de la enseñanza de las Matemáticas <br />Tema: Cine Matemático <br />Objetivo: Desarrollo de competencias lingüísticas y competencias matemáticas<br />Recursos didácticos: Película Pi fe en el caos <br />Actividades<br />Recreando la película <br />. (1) En el tren, Max escribe en el periódico las siguientes fórmulas A= πr2 C=2πr ¿A qué se refieren? ¿Por qué las escribe? (2) ¿Qué cálculo hace Max, mejor dicho, su mega-calculadora Euclides, para encontrar esta serie numérica? Max piensa:<br />12:45. Reformulo mis suposiciones:<br />1.-Las matemáticas son el lenguaje de la naturaleza.<br />2.-Todo puede representarse y entenderse con números.<br />3.-Al graficar cualquier sistema surgen patrones.<br />Por lo tanto, hay patrones en toda la naturaleza.<br />De acuerdo a esto y según lo que has visto en la película, ¿qué entiendes por modelos matemáticos?<br /> (3) ¿Para qué necesita Max un ordenador? ¿Qué es exactamente lo que hace con él?<br />¿Quién es Euclides en la película? ¿Quién fue en realidad?<br />¿Qué diferencia hay entre un numerólogo y un matemático?<br />El amigo de Max, Sol, le dice que si se obsesiona podrá encontrar el 216 en cualquier lado. ¿Cómo lo encontrarías en tu nombre?<br /> (4) ¿Cual es el valor del numero áureo?<br />En la película se habla del caos .¿Que relación tiene éste con la geometría fractal? 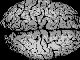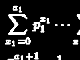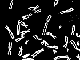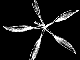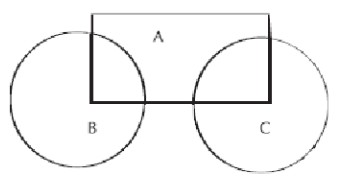<br />Pensamiento Algebraico ( Patrones )<br />Analice las siguientes igualdades y descubra la ley que se da entre ellas:<br /> 22 - 12 = 2(1) + 1 32 - 22 = 2(2) + 1 42 - 32 = 2(3) + 1 52 - 42 = 2(4) + 1 De acuerdo con la ley, 1002 - 992 es igual a<br />Pensamiento Aritmético <br />En una playa delimitamos las zonas A, B y C que se muestran en la figura. En la zona A hay 500 personas, 400 en la B y 300 en la C. En la zona común a las zonas A y B hay 50 personas mientras que en la zona común a las zonas A y C hay 100 personas. ¿Cuántas personas hay en total?
|
|
|
© Abel Martín & Marta Martín Sierra Esta página WEB se dedica exclusivamente a fines educativos, relacionando las "Matemáticas y el Cine". No existe ningún interés lucrativo. Las imágenes han sido tomadas de la TV y de Internet.
|
