|
REFERENCIAS MATEMÁTICAS
- Cuantos necios se han preguntado... -dice Hypatia con la voz en OFF- ¿por qué no caen las estrellas del cielo? Pero vosotros, que conocéis lo que dijeron los sabios, sabéis que las estrellas ni suben ni bajan, sólo giran de Este a Oeste, siguiendo el curso más perfecto jamás concebido: el círculo. Porque la perfección del círculo reina en los cielos, las estrellas jamás han caído ni caerán, pero... ¿y aquí, en la Tierra? Aquí los cuerpos sí caen y su movimiento no es circular, sino recto... ¿Qué misterioso prodigio se esconde bajo el suelo para que, todas las personas estén sobre él? Tras varias respuestas de los alumnos, concluye de manera tajante. - El centro sujeta todas las cosas y también las atrae. Si no existiera un centro, el Universo sería amorfo e infinito.
Teón e Hypatia están analizando resultados. No se sabe muy bien lo que hacen, pero la idea es mostrar que ellos están trabajando y haciendo cálculos. - ¿... llegas a 16 partiendo de 227? ...son 14 -dice Hypatia.
Amonio quiere demostrar que su Dios es el verdadero y que le permite pasar sobre las brasas de carbón sin quemarse... - Fijaos. Voy a caminar sobre el fuego. Si mi Dios es el verdadero, pasaré sin quemarme. Si por el contrario tus Dioses existen, me abrasarán como a un cerdo.
¿Podrías dar una explicación científica a este hecho?
La clásica pregunta en la que hay que dar una una respuesta, dejándola en forma de acertijo. - ¿Es cierto que eres cristiano? -le pregunta la filósofa a su esclavo Davo. - No sé que contestar ama. - ¿Por qué? - Si digo que sí te estaría mintiendo, pero si digo que no, le estaría mintiendo al amo, y no sé que es peor. - Entonces mejor no decir nada.
- Davo presenta en la clase una maqueta del sistema de Ptolomeo. - La Tierra. Es en centro del Cosmos... - explica Davo- y en torno a ella giran el Sol y las 5 errantes: Mercurio, Venus, Marte, Júpiter y Saturno, obstinadas en desobedecer la Ley del círculo... y sin embargo Ptolomeo nos demuestra que sí la obedecen. Si las vemos moverse como un bucle, es debido a la suma de 2 círculos: el que recorre alrededor de la Tierra y el círculo menor, propio de cada errante. No es el cielo el que se equivoca, nuestros ojos nos engañan.
- Los dioses deberían de haberme consultado antes de crearla -contesta Orestes- resulta todo muy caprichoso. ¿Por qué la suma de 2 círculos? No habría sido más perfecto que las errantes no erraran y que un sólo círculo diera sentido a todo. - Orestes- pregunta Sinesio- ¿Con qué autoridad juzgas tú la obra de Dios? Si censuras lo creado, censuras a nuestro señor y, nos ofendes. No sabéis de lo que habáis... ¡Ninguno! Hypatia interviene ante el cariz que toman los acontecimientos y pregunta, haciendo una alusión a los Elementos de Euclides. - Sinesio, cuál es la primera regla de Euclides -pregunta la matemática- - Si dos dos cosas son iguales a una tercera, todas son iguales entre sí -comenta un tanto contrariado. - Bien. ¿Y no sois ambos semejantes a mi? -ante la respuesta afirmativa de Sinesio y Orestes- Es más lo que nos une que lo que nos separa y, pase lo que pase en las calles, somos hermanos -en un intento de introducir la Lógica sobre el fanatismo.
- Ayer tratábamos el cono de Apolonio.- comenta Hypatia en su clase- hablábamos del círculo, de la elipse, de la parábola. Hoy examinaremos la hipérbola... - momento en el que es interrumpida por el anuncio de graves hechos que suceden en la ciudad.
Un buen momento para iniciar un repaso de estos elementos de la Geometría.
Hypatia y su padre juegan, utilizando un extraño dado hexagonal...
¿Conoces algún juego en el que se utilizase este tipo de dados?
He estado pensando en algo que me dijiste - le comenta Hypatia a Orestes -aquel día cuando censurabas el mecanismo celestial y lo llamaste caprichoso. -Sí, aunque, en realidad criticaba a Ptolomeo por complicarlo todo con sus epiciclos -responde Orestes- Pero, no sé. Quizá es que soy un simple. - No. Los cielos deben ser simples. ¿ Y si hubiera una explicación más sencilla para las errantes? - ¡La hay! -afirma un anciano que contempla el cielo- Pero es tan absurda, tan antigua, que nadie la tiene en cuenta. - ¿Hablas de Aristarco? - pregunta Hypatia - - Aristarco sostenía que la Tierra se mueve. El extraño comportamiento de las errantes no sería más que una ilusión óptica fruto de nuestro desplazamiento combinado con el suyo alrededor del sol. - Un modelo heliocéntrico. - Así es. El sol estaría en el centro, como le corresponde en calidad de astro rey. - Y la Tierra sería otra errante - continua la filósofa. - Su trabajo se perdió en el incendio de la biblioteca madre. Por eso debemos proteger ésta a cualquier precio. Nuestra biblioteca es todo lo que queda del saber de los hombres- añade el anciano. - Pero, cada vez que se deja caer un objeto... -comenta Davo- Si la Tierra se moviera, al dejar caer un objeto, caería detrás de nosotros. Y el viento siempre soplaría en contra.Y las aves se desorientarían al volar. - Ya he dicho que la hipótesis de Aristarco no tiene ni pies ni cabeza -mantiene el anciano- - Creo que se puede refutar lo que has dicho, pero ahora mismo, no sé cómo.
Investiga la importancia de la Biblioteca de Alejandría
Hypatia se dispone a probar todo esto que han comentado y refutar lo dicho por Davo. Quiero que cojas el saco- le dice Hypatia a Aspasio- y que subas al mástil. - Y ahora, señora, ¿me dirás para qué es todo esto? - pregunta Orestes. - Cuando Aspasio arroje el saco, la nave estará avanzando. Por lo tanto, el saco no caerá a los pies del mástil, sino un poco más atrás. Aproximadamente... aquí. Cuando sueltan el saco... -¡Sí! Ésta es la prueba definitiva. El saco se ha comportado como si el barco estuviese quieto. - ¿Y eso qué significa? - No lo sé. Pero el mismo Principio podría aplicarse a la Tierra. Podría moverse alrededor del sol sin que lo percibiéramos. - Aristarco -comenta Orestes- ¿Por qué te atormentas con eso? - Ptolomeo no es perfecto, pero funciona. - Orestes, si fuiste tú... Hace unos años no eras tan pragmático, prefecto. - Hace unos años hablaba antes de pensar.
Aspasio e Hypatia siguen dándole vueltas a los círculos sobre la arena. Una pregunta sigue sin ser contestada. - ¿Por qué cambia el sol? ¿Por qué cambia de tamaño del verano al invierno? -dice Hypatia. - ¿Quizá sea porque a veces está más cerca y a veces está más lejos? - Pero, Aspasio, verás. Según Aristarco, el Sol tiene que estar en el centro de todo. Y nosotros, la Tierra, viajando en círculo a su alrededor. Por lo tanto, y ésta es la clave, guardando siempre la misma distancia. Ahora bien, si aceptamos cambios en la distancia, ahora hay que sumar un epiciclo a la órbita de la Tierra. Ahora acercándonos, ahora alejándonos. Pero entonces caeríamos en la misma trampa que Ptolomeo. -Círculos sobre círculos -apostilla Aspasio. -¡Exacto! Pero yo no sé cómo resolver este conflicto.
En el recinto donde Hypatia da clase a los niños y a la que denomina su "pequeña biblioteca de Alejandría" podemos observar un fantástico "Cono de Apolonio", construido en madera. - Así es. Lo hice para enseñarles las cuatro curvas -le dice Hypatia al Obispo de Cirene- - El círculo, y la elipse... la parábola y la hipérbola -comenta Sinesio , mientras va desmontándolo- Es precioso. - Lo miro muchas veces y me pregunto por qué razón convive el círculo con formas tan impuras.
Comenta y describe el cono de Apolonio
- Hypatia, mira a tu alrededor -le dice Orestes a Hypatia-Muerte, horror, destrucción. Si los astros se movieran en círculo, ¿por qué compartirían su perfección con nosotros? Así que no nos movemos. - En círculo -replica Hypatia- No nos movemos... en círculo. No nos movemos en círculo. Desde Platón, todos ellos: Aristarco, Hiparco, Ptolomeo, todos han intentado armonizar las observaciones con órbitas circulares, pero... ¿Y si otra forma se oculta en los cielos. - Señora, no hay forma más pura que el círculo. Tú nos lo enseñaste. - Sí, lo sé, pero supón que la pureza del círculo nos ha impedido ver más un poco más allá, del mismo modo que el brillo del Sol no nos deja ver las estrellas. Debo empezar de nuevo, con nuevos ojos. Debo replantearlo todo. Todo.
Mientras Hypatia comenta con Aspasio diferentes teorías, según mira el cono de Apolonio intuye la posibilidad de órbitas elípticas y pasan de nuevo a la arena para explicar, de una forma muy didáctica, las características de una elipse. - Ata este extremo a esa antorcha -le pide Hypatia a Aspasio- imagina que esta es la Tierra y que cada una de estas llamas representan las dos posiciones del sol respecto a ella: la del invierno y la del verano. ¿Qué pasaría si ambas posiciones fueran los dos centros de un mismo círculo? - Pero, eso no es posible, ama. - Espera, ¿Qué sabemos del círculo? Sabemos que su centro equidista de cualquier punto de su perímetro. Sí, pero... ¿Y si divido ese centro en dos y lo que mantengo constante es la suma de sus distancias al perímetro? te lo demostraré. Mientras muevo esta vara por la cuerda, un segmento aumenta y el otro disminuye. Y viceversa. Por tanto la suma de ambos será constante. ¿Lo ves? ¿ Y si aplicamos esto al movimiento de la Tierra? ¿Qué...figura... obtendremos? ¡Una elipse! Una elipse con el sol en uno de sus focos. Porque, ¿qué es el círculo sino una elipse muy especial cuyos focos están tan próximos que parecen uno solo? ¿O tal vez estoy desvariando. Aspasio. Es decir, ¿es esto así? Quizá sólo esté... quizá esté... ¿Tú qué crees? - Bien pudiera ser, ama. - Muy bien, seguiremos con esto mañana.
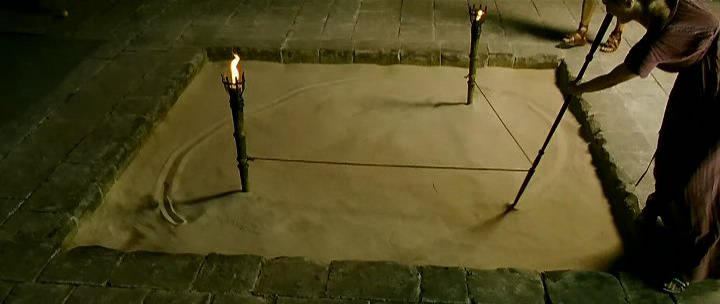
¿Las estaciones son causadas realmente por la pequeña excentricidad de la órbita terrestre? A lo largo de la película el personaje de Hypatia se emociona ante los textos de los Elementos de Euclides, el cono de Apolonio, el sistema geocéntrico de Ptolomeo y el heliocéntrico de Aristarco de Samos y se apasiona y empeña en resolver el enigma astronómico que plantean los planetas errantes vislumbrando en la elipse la solución que hallarán más de mil años después, en el siglo XVI, Copérnico y Kepler en su reformulación, hoy vigente, de la Teoría heliocéntrica de órbitas elípticas. Éste puede ser un importante comienzo para plantear en el aula toda una batería de cuestiones relativas tanto a la época como a las matemáticas: - Introducción a las cónicas. - Búsqueda de algún matemático romano importante. - Construcción de un reloj de sol. - Localización de mujeres matemáticas anteriores a Hypatia. - Plantearnos si existe realmente el cono de Apolonio. - La inclinación del eje de rotación de la Tierra... y un largo etcétera que irán conformando la base didáctica de ÁGORA EN EL AULA Estamos trabajando... |
|
|
© Abel Martín & Marta Martín Sierra Esta página WEB se dedica exclusivamente a fines educativos, relacionando las "Matemáticas y el Cine". No existe ningún interés lucrativo. Las imágenes han sido tomadas de la TV y de Internet.
|
