LA ESTADÍSTICA Y LOS NUEVOS MODELOS DE
CALCULADORAS GRÁFICAS
Abel Martín Álvarez (IES Pérez de Ayala de Oviedo, Asturias)
Jordi Baldrich Álvarez (Colegio Itaca de Barcelona)
Resumen | Introducción | Contenidos | Objetivos | Metodología | Prácticas | Evaluación | Reflexión final |
Presentamos el resultado de una experiencia llevada a cabo en el aula con alumnos de 15-17 años, donde podremos observar diferentes estrategias educativas que han surgido con la aparición de las nuevas tecnologías, para afrontar la enseñanza de las Matemáticas. Comprobaremos la posibilidad de ampliar contenidos al modificar los procedimientos de enseñanza; propondremos una nueva organización de la clase, coexistiendo, de forma simultánea, la matemática "tradicional" con otra más "innovadora", incluyendo nuevos tipos de actividades donde la reflexión, la toma de decisiones y la aplicación sean el objetivo fundamental.
La Organización de la enseñanza de las Matemáticas, y concretamente los temas de Estadística, han de cambiar inevitablemente sus objetivos, procedimientos y metodología para adecuar el impacto de la aparición de las nuevas tecnologías, entre las que vamos a destacar los nuevos modelos de máquinas de calcular, por su sencillez, pequeño tamaño, manejabilidad y precio, tal y como se está haciendo en todos los países "desarrollados", con el inconveniente de que la investigación para apoyar su didáctica está avanzando de forma muy lenta.
Este ha sido el motor fundamental que nos ha llevado a realizar esta experiencia "piloto" en un centro de Enseñanza Secundaria, el IES Pérez de Ayala de Oviedo (España), con alumnos de 15-17 años.

No vamos a enumerar los contenidos del tema "Estadística Bidimensional", pues son de todos conocidos, basta con mirar cualquier libro de texto. Simplemente mencionaremos que estas máquinas nos han permitido ampliar y profundizar en el estudio de la recta de Tukey, cuando existan "outliers", y la regresión no lineal.
Donde nos vamos a detener es en los dos apartados siguientes, objetivos y metodología, con la sugerencia de modificaciones y propuestas de nuevos enfoques, que permitan ajustar la enseñanza a los nuevos tiempos.
![]() Reconocer una variable estadística bidimensional y distinguir entre dependencia
funcional y dependencia estadística.
Reconocer una variable estadística bidimensional y distinguir entre dependencia
funcional y dependencia estadística.
![]() Saber
representar e interpretar una distribución bidimensional mediante una nube de
puntos.
Saber
representar e interpretar una distribución bidimensional mediante una nube de
puntos.
![]() Interpretar la correlación como una medida de relación lineal existente entre
dos variables.
Interpretar la correlación como una medida de relación lineal existente entre
dos variables.
![]() Reconocer las rectas de regresión como mejor ajuste a una nube de puntos.
Reconocer las rectas de regresión como mejor ajuste a una nube de puntos.
![]() Realizar predicciones, de forma crítica, partir de una recta de regresión,
cuando sea factible.
Realizar predicciones, de forma crítica, partir de una recta de regresión,
cuando sea factible.
![]() Facilitar la resolución de problemas, haciendo posible que el alumno dedique
mayor tiempo al análisis de la información inicial, a la toma de decisiones
sobre las acciones a realizar, a la verificación y análisis crítico de los
resultados, verdadero objetivo de los cursos preuniversitarios y universitarios.
Facilitar la resolución de problemas, haciendo posible que el alumno dedique
mayor tiempo al análisis de la información inicial, a la toma de decisiones
sobre las acciones a realizar, a la verificación y análisis crítico de los
resultados, verdadero objetivo de los cursos preuniversitarios y universitarios.
![]() Incorporar un elemento motivador como instrumento didáctico.
Incorporar un elemento motivador como instrumento didáctico.
![]() Proporcionar métodos alternativos para la resolución de problemas, estimulando
la capacidad de investigación del alumnado.
Proporcionar métodos alternativos para la resolución de problemas, estimulando
la capacidad de investigación del alumnado.
![]() Desarrollar la facultad del trabajo autónomo, pudiendo comprobar resultados,
confirmar conjeturas, sin la constante supervisión del profesor.
Desarrollar la facultad del trabajo autónomo, pudiendo comprobar resultados,
confirmar conjeturas, sin la constante supervisión del profesor.
![]() Fomentar el trabajo de grupo y la discusión.
Fomentar el trabajo de grupo y la discusión.
![]() Buscar una clase más participativa y reflexiva.
Buscar una clase más participativa y reflexiva.
![]() Eliminar, en lo posible, la carga que supone la gran cantidad de cálculos
matemáticos para llegar a tomar una decisión, que en muchas ocasiones, es el
objetivo fundamental perseguido.
Eliminar, en lo posible, la carga que supone la gran cantidad de cálculos
matemáticos para llegar a tomar una decisión, que en muchas ocasiones, es el
objetivo fundamental perseguido.
![]() Ejercitar y educar la mente para que el alumno, de forma espontánea, sea capaz
de tratar datos, buscar conclusiones, tomar decisiones... y, en definitiva,
¡¡pensar!!.
Ejercitar y educar la mente para que el alumno, de forma espontánea, sea capaz
de tratar datos, buscar conclusiones, tomar decisiones... y, en definitiva,
¡¡pensar!!.
![]() Posibilitar la ampliación de contenidos que hagan la unidad más "práctica y
transversal", relacionada en todo momento con el entorno cotidiano y el
comportamiento de la naturaleza donde, en la mayoría de las ocasiones, se
observan unas relaciones no lineales entre variables: regresión exponencial,
logarítmica, logística, potencial...
Posibilitar la ampliación de contenidos que hagan la unidad más "práctica y
transversal", relacionada en todo momento con el entorno cotidiano y el
comportamiento de la naturaleza donde, en la mayoría de las ocasiones, se
observan unas relaciones no lineales entre variables: regresión exponencial,
logarítmica, logística, potencial...
Tanto las clases teóricas como las prácticas (a través de la resolución y análisis de problemas) se imparten en el aula.
No es necesario desplazarse al aula de informática o a otra sala específica del instituto.
(a) Se comienza la actividad planteando a los alumnos una investigación sobre una situación de su entorno cotidiano, como por ejemplo:
- ¿Se puede descubrir alguna relación entre la estatura de los varones y sus padres?, ¿y de las chicas y sus madres? ¿y de los varones con la media de sus progenitores?... (Práctica 1)
(b) En el aula van a coexistir simultáneamente dos metodologías: una "clásica", que dispondrá de encerado (para explicar y registrar todos aquellos elementos que se crean oportunos) y otra más "innovadora" donde tomará el protagonismo la calculadora gráfica retroproyectable para que, de forma rápida y precisa, presente una visualización general, paralela al encerado.
(c) Los alumnos, sentados por parejas, dispondrán de una calculadora gráfica de mano (propia o aportada por el Departamento de Matemáticas), herramienta educativa matemática de última generación, de iguales características que la retroproyectable, donde podrán analizar sus hipótesis, buscar métodos alternativos a los presentados, confirmar conjeturas, resultados, hacer representaciones gráficas que refuercen visualmente los conceptos... a la vez que nos introducimos en el conocimiento y manejo de paquetes estadísticos en el aula y bajo el entorno Windows.
Uno de los alumnos será el que manipula la calculadora mientras el otro va aportando sugerencias, con el objetivo de fomentar la labor de respeto, organización y trabajo de grupo. Cada cierto periodo de tiempo "los roles" se van intercambiando.
(d) El profesor presenta el tema de una forma constructiva y participativa, desarrollando los contenidos al detalle, (covarianza, coeficiente de correlación, rectas de regresión...), sin centrarse en profundidad en los cálculos matemáticos (en los cursos inferiores) y con las justificaciones matemáticas adecuadas de cada uno de los conceptos (cursos superiores).
(e) El alumno planifica la obtención de los datos, los representa en forma de tablas de frecuencias, gráficamente en diagramas de dispersión, haciendo una primera interpretación intuitiva de la relación entre las variables, en cada caso, analizando si esa relación es lineal o no; si la relación es directa o inversa, si, con la información suministrada por la nube de puntos, se puede interpolar o extrapolar algún resultado concreto. (Práctica 2).
(f) A partir del estudio de las nubes de puntos obtenidas, el profesor introduce el concepto de correlación y el coeficiente de correlación como medida del grado de relación lineal entre las variables. El alumnado debe interpretar el significado de los distintos valores y signos del coeficiente de correlación y descubrir el tipo de relación entre las variables ante dichas situaciones. (Práctica 3 y Práctica 4).
(g) Entre varias nubes de puntos, situaciones y varios coeficientes de correlación el alumno debe asignarlos correctamente. Con la calculadora se pueden confirmar los resultados aportados por los alumnos a través de problemas que el profesor trae almacenados en la máquina. (Práctica 5).
(h) Se buscan, mediante métodos gráficos, rectas que se ajusten a las distribuciones bidimensionales estudiadas y relacionan las medias de las dos variables con la recta que más se ajuste. Mediante esta aproximación intuitiva el profesor introduce el concepto de recta de regresión. También es importante que el alumno realice extrapolaciones utilizando la recta de regresión, estimando los márgenes de error posible y grado de fiabilidad de las predicciones. (Práctica 6).
(i) Ante la presencia de "outliers" podremos comprobar la importancia de la recta de Tukey y su fácil estudio con la ayuda de una calculadora gráfica. Con lápiz y papel es inviable y nos llevaría horas. (Práctica 7).
(j) Esta herramienta permite ajustar datos a cualquier función lineal o no lineal, estimando los parámetros para un criterio de optimización (suma de los mínimos cuadrados), convirtiéndose en un instrumento de modelización utilizable en contextos muy diversos (finanzas, marketing, medicina,...). (Práctica 8).
(k) Una vez finalizada la presentación teórica y práctica del tema, hemos propuesto un cuestionario de preguntas, de contestación corta, con el objetivo de comprobar el grado de comprensión de los conceptos. La respuesta fue individual, trabajada en casa y registrada en el cuaderno, para una posterior puesta en común y discusión en clase, actuando el profesor como moderador, buscando siempre el debate y la reflexión. (Práctica 9).

(l) Para finalizar, se han trabajado 3 tipos de ACTIVIDADES DE CONSOLIDACIÓN:
- ACTIVIDADES tipo A (16-17 años), en las que el alumno puede utilizar la calculadora como herramienta auxiliar para realizar operaciones y comprobar y contrastar resultados e hipótesis, justificando mediante cálculos matemáticos, en todo momento, lo que hace.
- ACTIVIDADES tipo B (15-16 años), en las que la calculadora cobra total protagonismo, con preguntas diseñadas para que, después de introducir los datos en la máquina, el alumno se centre en las respuestas, en la reflexión y donde el objetivo fundamental es ENTENDER los conceptos y la APLICACIÓN de los resultados a las situaciones propuestas.
- ACTIVIDADES INDAGATORIAS tipo TEST, con una respuesta a elegir de entre varias.
![]() A continuación propondremos diversos modelos de
prácticas en esta línea, que pueden servir para dar ideas al profesorado,
auténtico protagonista del enfoque diario en el aula.
A continuación propondremos diversos modelos de
prácticas en esta línea, que pueden servir para dar ideas al profesorado,
auténtico protagonista del enfoque diario en el aula.
![]() El alumno realizará, de forma individual, un
trabajo de investigación (tema libre) acerca de la comprobación del grado de
relación entre dos variables, que debe culminar con la realización de un informe
completo con todas las conclusiones y análisis obtenidos, simplificando lo más
posible los cálculos matemáticos, utilizando las herramientas mecánicas
habituales del aula, así como un breve comentario de lo que se está estudiando,
con apoyo bibliográfico, dándole un carácter transversal al tema y a la
asignatura.
El alumno realizará, de forma individual, un
trabajo de investigación (tema libre) acerca de la comprobación del grado de
relación entre dos variables, que debe culminar con la realización de un informe
completo con todas las conclusiones y análisis obtenidos, simplificando lo más
posible los cálculos matemáticos, utilizando las herramientas mecánicas
habituales del aula, así como un breve comentario de lo que se está estudiando,
con apoyo bibliográfico, dándole un carácter transversal al tema y a la
asignatura.
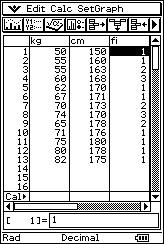
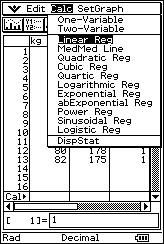
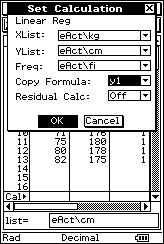
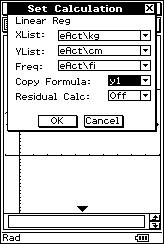
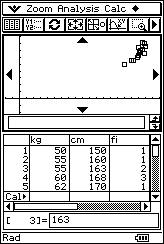
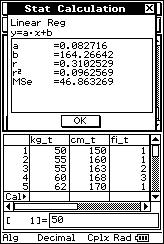
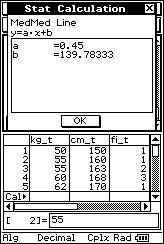
![]() Se han medido los pesos ("x" expresados en
kilogramos) y las tallas ("y" expresadas en centímetros) de 20 personas,
obteniéndose los siguientes resultados:
Se han medido los pesos ("x" expresados en
kilogramos) y las tallas ("y" expresadas en centímetros) de 20 personas,
obteniéndose los siguientes resultados:
(50, 150), (55, 160), (55, 163), (55, 163), (60, 168), (60, 168), (60, 168), (62, 170), (67, 171), (70, 173), (70, 173), (74, 170), (74, 170), (74, 170), (65, 178), (65, 178), (71, 176), (75, 180), (80, 178), (82, 175).
![]() Averigua e interpreta,
con la ayuda de la calculadora, el valor de los diferentes parámetros
estadísticos unidimensionales, acerca de los pesos (P) y las tallas (T) de las
personas.
Averigua e interpreta,
con la ayuda de la calculadora, el valor de los diferentes parámetros
estadísticos unidimensionales, acerca de los pesos (P) y las tallas (T) de las
personas.
|
|
|
|
|
|
|
|
|
|
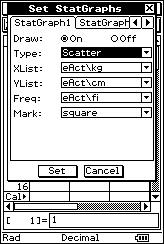
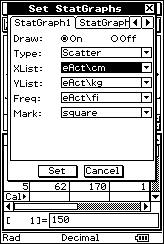
![]() Representa los pares de valores de la distribución en un sistema de
ejes cartesianos.
Representa los pares de valores de la distribución en un sistema de
ejes cartesianos.
 |
 |
 |
 |
|
|
|
|
|
![]() Interpreta, de forma intuitiva, la relación entre las variables.
Interpreta, de forma intuitiva, la relación entre las variables.
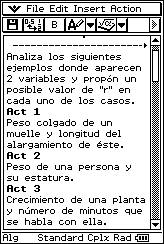
![]() Analiza los siguientes ejemplos donde aparecen
dos variables y propón un posible valor de "r" en cada uno de los casos.
Analiza los siguientes ejemplos donde aparecen
dos variables y propón un posible valor de "r" en cada uno de los casos.
![]() Peso colgado de un muelle y longitud del alargamiento de éste.
Peso colgado de un muelle y longitud del alargamiento de éste.
![]() Peso de una persona y su estatura.
Peso de una persona y su estatura.
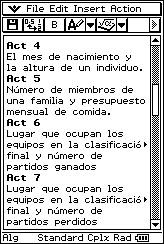
![]() El mes de nacimiento y la altura de un individuo.
El mes de nacimiento y la altura de un individuo.
![]() Lugar que ocupan los equipos en la clasificación final y número de
partidos ganados.
Lugar que ocupan los equipos en la clasificación final y número de
partidos ganados.
![]() Lugar que ocupan los equipos en la clasificación final y número de
partidos perdidos.
Lugar que ocupan los equipos en la clasificación final y número de
partidos perdidos.
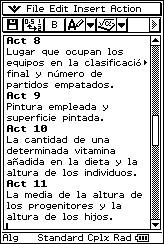
![]() Lugar que ocupan los equipos en la clasificación final y número de
partidos empatados.
Lugar que ocupan los equipos en la clasificación final y número de
partidos empatados.
 |
 |
 |
 |
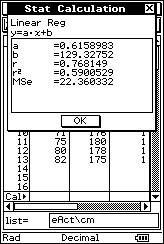
![]() Cuantifica, de manera objetiva, precisa y matemática, la relación
lineal existente entre los pesos ("x" expresados en kg) y las tallas ("y"
expresadas en cm).
Cuantifica, de manera objetiva, precisa y matemática, la relación
lineal existente entre los pesos ("x" expresados en kg) y las tallas ("y"
expresadas en cm).
![]() ¿Cómo se llama el parámetro que se utiliza habitualmente para medirlo?.
¿Cómo se llama el parámetro que se utiliza habitualmente para medirlo?.
 |
 |
 |
 |
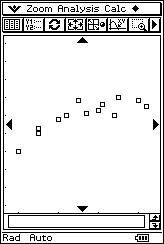
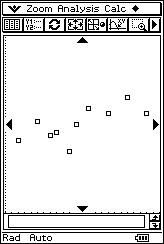
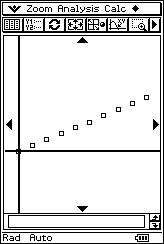
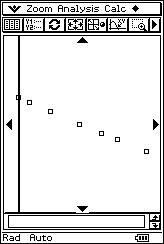
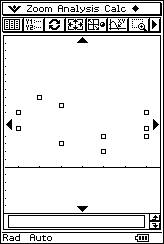
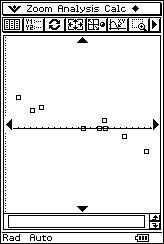
![]() El profesor propondrá, sucesivamente, con la
calculadora retroproyectable ocho nubes de puntos y ocho posibles valores de
"r". El alumno tiene que asignar a cada nube de puntos la correlación lineal que
le corresponde.
El profesor propondrá, sucesivamente, con la
calculadora retroproyectable ocho nubes de puntos y ocho posibles valores de
"r". El alumno tiene que asignar a cada nube de puntos la correlación lineal que
le corresponde.
 |
r = 0.76 r = 0.69 r = 1 r = - 0.99 |
r = - 0.33 r = - 0.95 r = 0.01 r = - 0.94 |
 |
 |
 |
 |
 |
 |
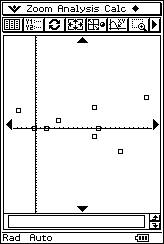 |
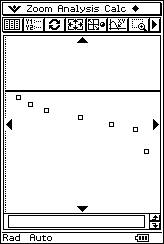 |
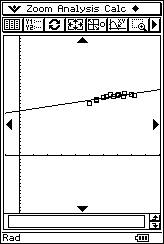
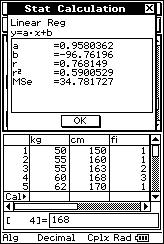
![]() Busca, (con LÁPIZ Y PAPEL, en cursos superiores, y con calculadora, en
los cursos inferiores), la ecuación de la recta que mejor se ajuste a la nube de
puntos.
Busca, (con LÁPIZ Y PAPEL, en cursos superiores, y con calculadora, en
los cursos inferiores), la ecuación de la recta que mejor se ajuste a la nube de
puntos.
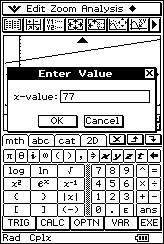
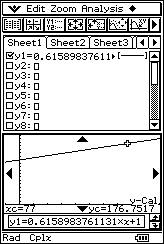
![]() Si una persona pesa 77 kg, ¿cuánto se espera que mida?. Justifica la
respuesta.
Si una persona pesa 77 kg, ¿cuánto se espera que mida?. Justifica la
respuesta.
![]() Comenta la fiabilidad de las predicciones.
Comenta la fiabilidad de las predicciones.
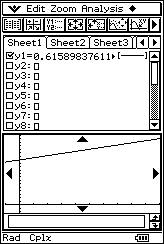
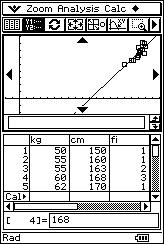
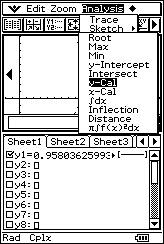
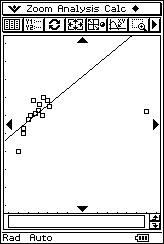
![]() Dibuja la recta de regresión de "y" sobre "x" sobre la nube de puntos
para comprobar como se ajusta.
Dibuja la recta de regresión de "y" sobre "x" sobre la nube de puntos
para comprobar como se ajusta.
 |
 |
 |
 |
 |
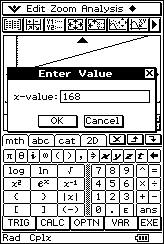 |
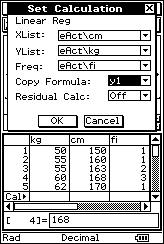
![]() Si una persona pesa 168 kg, ¿cuánto se espera que mida?.
Si una persona pesa 168 kg, ¿cuánto se espera que mida?.
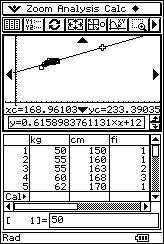 |
 |
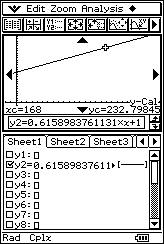 |
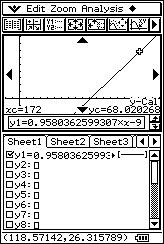
![]() Calcula la recta de regresión de "x" sobre "y". Justifica la respuesta.
Calcula la recta de regresión de "x" sobre "y". Justifica la respuesta.
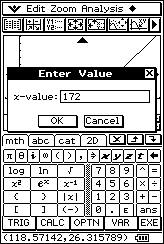
![]() Si una persona mide 172 cm, ¿cuánto se espera que pese?.
Si una persona mide 172 cm, ¿cuánto se espera que pese?.
 |
 |
 |
 |
 |
 |
 |
 |
![]() Si al problema le añadimos un nuevo dato (180,
172). Busca la nueva recta de regresión. Explica brevemente lo que has hecho.
Si al problema le añadimos un nuevo dato (180,
172). Busca la nueva recta de regresión. Explica brevemente lo que has hecho.
 |
 |
 |
 |
 |
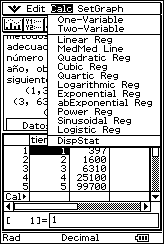
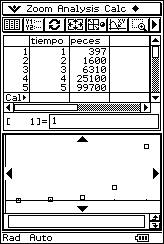
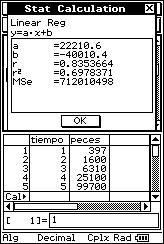
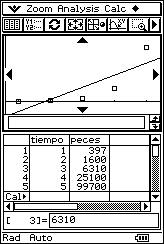
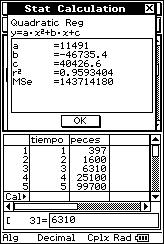
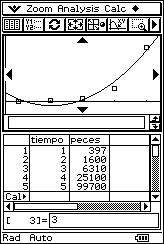
![]() Hace 5 años se ha comenzado a repoblar un lago con una nueva especie de
peces. En ese momento se introdujeron 100 ejemplares de esta nueva especie y se
ido observando, a través de métodos estadísticos adecuados de conteo, el número
de peces cada año, obteniéndose los siguientes datos:
Hace 5 años se ha comenzado a repoblar un lago con una nueva especie de
peces. En ese momento se introdujeron 100 ejemplares de esta nueva especie y se
ido observando, a través de métodos estadísticos adecuados de conteo, el número
de peces cada año, obteniéndose los siguientes datos:
(1, 397), (2, 1600), (3, 6310), (4, 25100), (5, 99700).



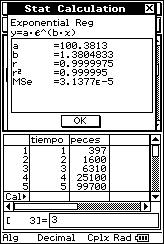
![]() Analiza si existe algún tipo de regresión no
lineal que se ajuste mejor a los datos de la muestra que el lineal.
Analiza si existe algún tipo de regresión no
lineal que se ajuste mejor a los datos de la muestra que el lineal.
 |
 |
 |
 |
 |
 |
 |
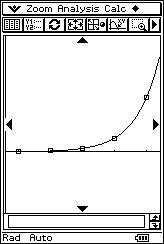 |
![]() ¿Cuánto tiempo habrán de esperar para que haya 300 000 ejemplares?.
¿Cuánto tiempo habrán de esperar para que haya 300 000 ejemplares?.
|
|
|
![]() Teniendo en cuenta que existe una presión ambiental (espacio,
contaminación, alimentos, competencia etc.) que modifica dicha forma de crecer,
limitándolo, ¿conoces algún tipo de regresión que haga una predicción del
crecimiento más fiable? ¿cómo se llama?.
Teniendo en cuenta que existe una presión ambiental (espacio,
contaminación, alimentos, competencia etc.) que modifica dicha forma de crecer,
limitándolo, ¿conoces algún tipo de regresión que haga una predicción del
crecimiento más fiable? ¿cómo se llama?.
|
|
|
![]() Contesta brevemente a las siguientes cuestiones
de forma razonada:
Contesta brevemente a las siguientes cuestiones
de forma razonada:
![]() Explica qué significa que la correlación lineal entre dos variables sea
positiva. Pon un ejemplo.
Explica qué significa que la correlación lineal entre dos variables sea
positiva. Pon un ejemplo.
![]() ¿Existe algún punto por el que siempre pase la recta de regresión?.
¿Existe algún punto por el que siempre pase la recta de regresión?.
![]() ¿Qué quiere decir que la correlación lineal entre dos variables es muy
débil?. Pon un ejemplo.
¿Qué quiere decir que la correlación lineal entre dos variables es muy
débil?. Pon un ejemplo.
![]() ¿Tiene sentido calcular la recta de regresión de una distribución
bidimensional sabiendo que el coeficiente de correlación es r = 0.12?.
¿Tiene sentido calcular la recta de regresión de una distribución
bidimensional sabiendo que el coeficiente de correlación es r = 0.12?.
![]() Dada una nube de puntos, ¿existe algún método que permita obtener
aproximadamente el valor de "r" sin necesidad de realizar ningún cálculo?.
Dada una nube de puntos, ¿existe algún método que permita obtener
aproximadamente el valor de "r" sin necesidad de realizar ningún cálculo?.
![]() La correlación sólo es válida para valores próximos a los datos.
¿Porqué?.
La correlación sólo es válida para valores próximos a los datos.
¿Porqué?.
Nota: en total, el cuestionario consta de 26 preguntas.
![]() Trabajo de investigación
Trabajo de investigación
![]() Prueba objetiva escrita (según el nivel) en la
que incluimos actividades con y sin justificaciones matemáticas y preguntas
indagatorias, tipo test.
Prueba objetiva escrita (según el nivel) en la
que incluimos actividades con y sin justificaciones matemáticas y preguntas
indagatorias, tipo test.
La inclusión de estas nuevas herramientas educativas matemáticas de última generación ha supuesto un enriquecimiento en la adquisición de conceptos y en la búsqueda de métodos alternativos a los tradicionales y que se ha traducido en unos mejores resultados académicos con respecto a los correspondientes grupos "testigo", donde no se han utilizado en ningún momento este tipo de máquinas. Se observó una mejor predisposición hacia la asignatura, más en consonancia con la realidad que rodea al alumno, contrastada con los cuestionarios realizados al final del proyecto.
Es hora de comenzar a derribar esos "muros infranqueables" que presenta la enseñanza secundaria, y no digamos la primaria, esclava de los algoritmos y del cálculo mecánico que, como profesores, vamos transmitiendo de generación en generación...
¡¡Pensemos en nuestros alumnos y en todo aquello que nos horrorizaba en el pasado...
¡¡¡Qué rollo... ahora toca matemáticas!!!
... y cambiémoslo por:
¡¡Bien... ahora toca Matemáticas!!
con el objetivo fundamental de

¡¡ PENSAR !!